 Sieve Diagrams
Sieve Diagrams
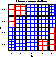
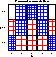
A sieve diagram shows the frequencies in a two-way contingency table in relation to expected frequencies under independence, and highlights the
pattern of association between the row and column variables.
The sieve diagram was proposed by Riedwyl and Schüpbach in a technical report in
1983 and later called a parquet diagram (Riedwyl and Schüpbach, 1994).
Constructing the sieve diagram
In this display:
- A unit square is divided into rectangles, one for each cell in the
contingency table.
- The height of each rectangle in row i is proportional to the marginal
frequency in that row ( f i+ ); the width of each rectangle in column j is proportional to the marginal frequency in that column ( f +j ).
- Hence, the area of each rectangle is proportional to the expected frequency,
e ij = (f i+ f +j ) / f ++
under the hypothesis that the row and column variables are independent.
- The observed frequency in each cell is shown by the number of squares drawn in each rectangle.
- Hence, the difference
between observed and expected frequency appears as the density of
shading, using color to indicate whether the deviation from
independence is
positive (blue) or negative (red).
Examples, Demo, Software
- Examples
- This section from my short course, Categorical Data Analysis with Graphics shows several examples.
- Form-based Demo
- Enter your own data, and receive the graphic output.
- sieve.sas
- The SAS/IML program which draws sieve diagrams. There's also a Sieve diagram sample (sievedemo.sas).
- sieveplot.sas
- SAS macro for sieve diagrams.
Michael Friendly
Email: friendly AT yorku DOT ca
 Sieve Diagrams
Sieve Diagrams
