
This page aims to walk you through the procedures and analyses run during our presentation on “Recent Advances in Visualizing Multivariate Linear Models” at the 2013 Statistical Society of Canada annual conference. The following examples use three primary datasets: iris (a base dataset), and Pottery and Rohwer, both of which are included in the heplots package.
library(heplots)
head(iris)
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1 5.1 3.5 1.4 0.2 setosa
## 2 4.9 3.0 1.4 0.2 setosa
## 3 4.7 3.2 1.3 0.2 setosa
## 4 4.6 3.1 1.5 0.2 setosa
## 5 5.0 3.6 1.4 0.2 setosa
## 6 5.4 3.9 1.7 0.4 setosa
summary(iris)
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## Min. :4.30 Min. :2.00 Min. :1.00 Min. :0.1 setosa :50
## 1st Qu.:5.10 1st Qu.:2.80 1st Qu.:1.60 1st Qu.:0.3 versicolor:50
## Median :5.80 Median :3.00 Median :4.35 Median :1.3 virginica :50
## Mean :5.84 Mean :3.06 Mean :3.76 Mean :1.2
## 3rd Qu.:6.40 3rd Qu.:3.30 3rd Qu.:5.10 3rd Qu.:1.8
## Max. :7.90 Max. :4.40 Max. :6.90 Max. :2.5
head(Pottery)
## Site Al Fe Mg Ca Na
## 1 Llanedyrn 14.4 7.00 4.30 0.15 0.51
## 2 Llanedyrn 13.8 7.08 3.43 0.12 0.17
## 3 Llanedyrn 14.6 7.09 3.88 0.13 0.20
## 4 Llanedyrn 11.5 6.37 5.64 0.16 0.14
## 5 Llanedyrn 13.8 7.06 5.34 0.20 0.20
## 6 Llanedyrn 10.9 6.26 3.47 0.17 0.22
summary(Pottery)
## Site Al Fe Mg Ca Na
## AshleyRails: 5 Min. :10.1 Min. :0.92 Min. :0.53 Min. :0.010 Min. :0.030
## Caldicot : 2 1st Qu.:11.9 1st Qu.:1.70 1st Qu.:0.67 1st Qu.:0.060 1st Qu.:0.050
## IsleThorns : 5 Median :13.8 Median :5.46 Median :3.83 Median :0.155 Median :0.150
## Llanedyrn :14 Mean :14.5 Mean :4.47 Mean :3.14 Mean :0.147 Mean :0.159
## 3rd Qu.:17.4 3rd Qu.:6.59 3rd Qu.:4.50 3rd Qu.:0.215 3rd Qu.:0.215
## Max. :20.8 Max. :7.09 Max. :7.23 Max. :0.310 Max. :0.540
head(Rohwer)
## group SES SAT PPVT Raven n s ns na ss
## 1 1 Lo 49 48 8 1 2 6 12 16
## 2 1 Lo 47 76 13 5 14 14 30 27
## 3 1 Lo 11 40 13 0 10 21 16 16
## 4 1 Lo 9 52 9 0 2 5 17 8
## 5 1 Lo 69 63 15 2 7 11 26 17
## 6 1 Lo 35 82 14 2 15 21 34 25
summary(Rohwer)
## group SES SAT PPVT Raven n
## Min. :1.00 Hi:32 Min. : 1.0 Min. : 40.0 Min. : 8.0 Min. : 0.00
## 1st Qu.:1.00 Lo:37 1st Qu.:14.0 1st Qu.: 59.0 1st Qu.:12.0 1st Qu.: 1.00
## Median :1.00 Median :35.0 Median : 71.0 Median :14.0 Median : 3.00
## Mean :1.46 Mean :38.9 Mean : 72.1 Mean :14.1 Mean : 3.49
## 3rd Qu.:2.00 3rd Qu.:58.0 3rd Qu.: 82.0 3rd Qu.:16.0 3rd Qu.: 5.00
## Max. :2.00 Max. :99.0 Max. :105.0 Max. :21.0 Max. :20.00
## s ns na ss
## Min. : 0.00 Min. : 3 Min. :11.0 Min. : 8.0
## 1st Qu.: 4.00 1st Qu.:10 1st Qu.:18.0 1st Qu.:16.0
## Median : 7.00 Median :14 Median :25.0 Median :21.0
## Mean : 7.07 Mean :14 Mean :23.3 Mean :19.8
## 3rd Qu.:10.00 3rd Qu.:18 3rd Qu.:27.0 3rd Qu.:24.0
## Max. :18.00 Max. :28 Max. :35.0 Max. :32.0
The script is organized sequentially based upon the plots used in our presentation. However, plots shown during the background overview that are repeated in a later section are only shown in the pertinent subsection. The structure is as follows:
To contrast the novel developments in data visualization techniques, we begin by demonstrating some traditional techniques and how they are used to convey information about more simplistic designs.
Our first graphics demonstrate some of the traditional bivariate approaches to visualizing data. These figures are created using the lattice package, which allows the user to request a data concentration ellipse be superimposed on the plots.
library(lattice)
library(latticeExtra)
# A simple grouped scatterplot:
xyplot(Sepal.Length/10 ~ Petal.Length/10, group = Species, data = iris,
# Define axes:
xlab = "Petal length (mm)", ylab = "Sepal length (mm)",
# Define legend parameters:
auto.key = list(x = .1, y = .8, corner = c(0, 0)),
scales = "free", par.settings=list(superpose.symbol=list(pch=1:3)))
# A grouped scatterplot with 95% data concentration ellipses:
xyplot(Sepal.Length/10 ~ Petal.Length/10, groups=Species, data = iris,
# Define axes:
xlab = "Petal length (mm)", ylab = "Sepal length (mm)",
# Define legend parameters:
auto.key = list(x = .1, y = .8, corner = c(0, 0)), scales = "free",
par.settings = list(superpose.symbol = list(pch=c(1:13)), superpose.line = list(lwd=2, lty=1:3)),
# Superimpose data ellipse on the scatterplot:
panel = function(x, y, ...) {
panel.xyplot(x, y, ...)
panel.ellipse(x, y, ...)
}
)
With additional variables (the iris dataset contains four continuous variables that are of interest, and one categorical variable that is used for grouping), we can look at each of the bivariate relationships in turn. For instance, using the car package, we can produce a scatterplot matrix that is annotated to include data concentration ellipses for each group:
library(car)
scatterplotMatrix(~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width | Species,
data = iris, diagonal = "none", smoother = FALSE, reg.line = lm,
ellipse = TRUE, by.groups = TRUE)
Finally, utilizing a data reduction technique, we can look at a biplot, which demonstrates the relationship between the variables in terms of how each aids in accounting for the maximum amount of variation found in the data.
# A biplot showing the maximum total variation by species:
library(bpca)
library(car)
iris.pca <- bpca(iris[,-5], method = "sqrt", scale = TRUE)
scores <- iris.pca$coord$objects[,1:2]
col <- c('blue', 'darkgreen', 'red')[unclass(iris$Species)]
plot(iris.pca,
var.factor = .24, var.cex = 1.2, var.col = "black", lwd = 2,
obj.names = FALSE, obj.cex = 1, obj.col = col,
obj.pch = (15:17)[unclass(iris$Species)], xpd = TRUE)
dataEllipse(scores, add=TRUE, levels=0.68, col="gray", plot.points=FALSE)
dataEllipse(scores, groups=iris$Species, add=TRUE, levels=0.68, col=unique(col), plot.points=FALSE)
This narrative follows our substantive example, using the Romano-British Pottery data, which has five continuous variables designating concentration of minerals in a particular piece and one categorical variable regarding the site at which it was found.
pottery.mod <- lm(cbind(Al, Fe, Mg, Ca, Na) ~ Site, data = Pottery)
pottery.man <- Manova(pottery.mod)
summary(pottery.man)
##
## Type II MANOVA Tests:
##
## Sum of squares and products for error:
## Al Fe Mg Ca Na
## Al 48.2881 7.08007 0.60801 0.10647 0.58896
## Fe 7.0801 10.95085 0.52706 -0.15519 0.06676
## Mg 0.6080 0.52706 15.42961 0.43538 0.02762
## Ca 0.1065 -0.15519 0.43538 0.05149 0.01008
## Na 0.5890 0.06676 0.02762 0.01008 0.19929
##
## ------------------------------------------
##
## Term: Site
##
## Sum of squares and products for the hypothesis:
## Al Fe Mg Ca Na
## Al 175.610 -149.296 -130.810 -5.8892 -5.3723
## Fe -149.296 134.222 117.745 4.8218 5.3259
## Mg -130.810 117.745 103.351 4.2092 4.7105
## Ca -5.889 4.822 4.209 0.2047 0.1548
## Na -5.372 5.326 4.711 0.1548 0.2582
##
## Multivariate Tests: Site
## Df test stat approx F num Df den Df Pr(>F)
## Pillai 3 1.55 4.30 15 60.00 2.41e-05 ***
## Wilks 3 0.01 13.09 15 50.09 1.84e-12 ***
## Hotelling-Lawley 3 35.44 39.38 15 50.00 < 2e-16 ***
## Roy 3 34.16 136.64 5 20.00 9.44e-15 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
op <- par(mfrow = c(2,3))
boxplot(Al ~ Site, data = Pottery, main = "Al")
boxplot(Fe ~ Site, data = Pottery, main = "Fe")
boxplot(Mg ~ Site, data = Pottery, main = "Mg")
boxplot(Ca ~ Site, data = Pottery, main = "Ca")
boxplot(Na ~ Site, data = Pottery, main = "Na")
par(op)
The univariate displays are limited - they show the variation in the elements at the different sites, but they do not show which elements group together. A more novel approach for working with a multivariate linear models with two dependent variables is to use a Hypothesis-Error (HE) plot. In this plot, we take the regression of petal length and sepal length on species from the iris dataset.
iris.mod <- lm(cbind(Petal.Length, Sepal.Length) ~ Species, data = iris)
heplot(iris.mod, xlab = "Petal Length in cm.", ylab = "Sepal length in cm.", size = "effect")
Similarly, with the Pottery data, we can look at 2-D HE plots to show how the sites differ on two elements at a time. These plots can also be configured to display different scaling coefficients for the plotting of the hypothesis ellipse relative to the error ellipse.
# Obtain limits from the model:
pot <- heplot(pottery.mod)
# 2-D HE Plot for Aluminum and Iron with "Effect" Scaling (with annotations):
heplot(pottery.mod, size="effect.size",
xlim = pot$xlim, ylim = pot$ylim, main = "Pottery data: Al and Fe",
fill = c(TRUE, TRUE), fill.alpha = 0.05, cex.lab = 1.25)
# Add annotations:
label <- expression(paste("Effect scaling:", H / df[e]))
text(12.6, 7.2, label, col = "blue", cex = 1.5, pos = 4)
label <- expression( E / df[e])
text(16.8, 5.2, label, col = "red", cex = 1.5, pos = 4)
# Addition of the ellipse generated with "Significance" Scaling:
heplot(pottery.mod, add = TRUE, col = "darkgreen", fill = c(FALSE, TRUE), fill.alpha = 0.1)
label <- expression(paste("Significance scaling: H / ", lambda[alpha], df[e]))
text(10.6, 8.7, label, col = "darkgreen", cex = 1.5, pos = 4)
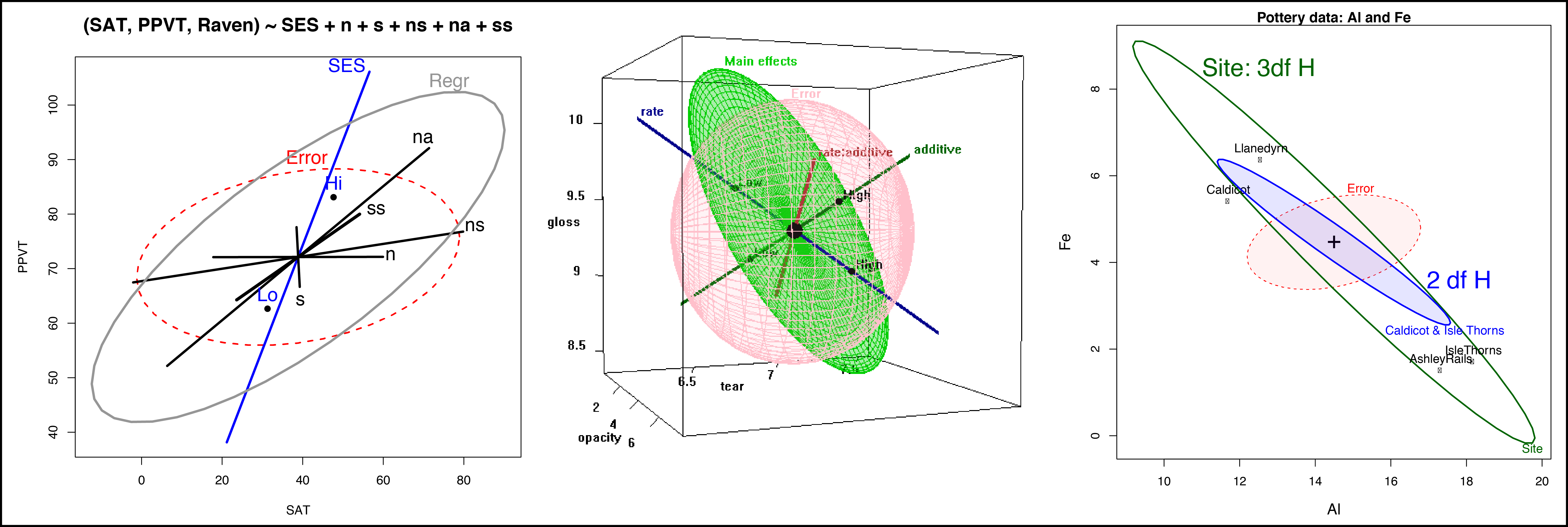
The HE plot is also amenable to visualizing particular contrasts and linear hypotheses.
# 2-D HE plot for Aluminum and Iron with 3 degree of freedom hypothesis:
heplot(pottery.mod, col = c("red", "darkgreen"), main = "Pottery data: Al and Fe",
fill = c(TRUE,FALSE), fill.alpha = 0.05, cex.lab = 1.25)
# Add annotation:
text(12.5, 8.5, "Site: 3df H", col = "darkgreen", cex = 2)
heplot(pottery.mod, col = c("red", "darkgreen"), main = "Pottery data: Al and Fe",
fill = c(TRUE,FALSE), fill.alpha = 0.05, cex.lab = 1.25)
# Add annotation:
text(12.5, 8.5, "Site: 3df H", col = "darkgreen", cex = 2)
# Addition of a 2 degree of freedom hypothesis:
heplot(pottery.mod, terms = FALSE, add = TRUE, col = "blue",
hypotheses = list("Caldicot & Isle Thorns" = c("SiteCaldicot = 0", "SiteIsleThorns = 0")),
fill = c(FALSE, TRUE), fill.alpha = 0.1)
# Add annotation:
text(17.8, 3.6, "2 df H", col="blue", cex=2)
heplot(pottery.mod, col = c("red", "darkgreen"), main = "Pottery data: Al and Fe",
fill = c(TRUE,FALSE), fill.alpha = 0.05, cex.lab = 1.25)
# Add annotation:
text(12.5, 8.5, "Site: 3df H", col = "darkgreen", cex = 2)
# Addition of a 2 degree of freedom hypothesis:
heplot(pottery.mod, terms = FALSE, add = TRUE, col = "blue",
hypotheses = list("Caldicot & Isle Thorns" = c("SiteCaldicot = 0", "SiteIsleThorns = 0")),
fill = c(FALSE, TRUE), fill.alpha = 0.1)
# Add annotation:
text(17.8, 3.6, "2 df H", col="blue", cex=2)
# Addition of a 1 degree of freedom hypothesis:
heplot(pottery.mod, terms = FALSE, add = TRUE, col="brown",
hypotheses=list("C-A" = "SiteCaldicot", "I-A" = "SiteIsleThorns"))
text(13.1, 4.5, "1 df H", col="brown", cex=1.7)
With more than two response variables, we can also visualize all pairs using a generalization of the scatterplot matrix:
# With the iris dataset:
iris.mod <- lm(cbind(Sepal.Length, Sepal.Width, Petal.Length, Petal.Width) ~ Species, data = iris)
pairs(iris.mod)
# With the Pottery dataset:
pairs(pottery.mod, fill=TRUE, fill.alpha=0.1)
Finally, we can also produce an interactive visualization that yields information on how three variables behave simultaneously with heplot3d():
# Uncomment the heplot3d line to produce the plot.
# It can be rotated to view the data cloud from all sides.
# Note: This visualization will load in a new window.
# heplot3d(pottery.mod)
Unfortunately, the 3D plot can only show three variables at a time, and as such cannot express all of the relationships at play.
HE plots are also useful in multivariate multiple regression, where the predictor variables are quantitative. In this design, we often test two primary sets of hypotheses: one, to see is all coefficients for each of the responses is zero (overall test); and two, for the significance of the individual predictor slopes.
This process can be demonstrated using Rohwer's data on paired-associate (PA) tasks, the five continuous predictors, and how they measure intelligence and achievement, which was captured using three scales, the SAT, the Peabody Picture Vocabulary Test, and the Raven Progressive Matrices test.
# Multivariate regression model for low SES students:
rohwer.ses2 <- lm(cbind(SAT, PPVT, Raven) ~ n + s + ns + na + ss, data = Rohwer, subset = SES=="Lo")
# Test of infidivudal predicators (lines) and overall test (blue ellipse):
he <- heplot(rohwer.ses2, col=c("red", rep("black", 5), "blue"),
hypotheses = list("Overall: B = 0" = c("n", "s", "ns", "na", "ss")),
cex = 1.25, fill = c(TRUE, TRUE), fill.alpha = c(.05, .1),
xlab = "Student Achievement Test",
ylab = "Peabody Picture Vocabulary Test",
cex.lab = 1.25, xlim = c(-10, 70), ylim = c(30, 90))
A similar approach can be taken with an MANVOCA design. First, we use Rohwer's data on both low SES students (the previous model) and high SES students to fit seperate regressions for each group.
rohwer.ses1 <- lm(cbind(SAT, PPVT, Raven) ~ n + s + ns + na + ss, data = Rohwer, subset = SES == "Hi")
# HE Plot for Low SES Students:
he2 <- heplot(rohwer.ses2, col=c("red", rep("black",5), "blue"),
hypotheses = list("B=0, Low SES" = c("n", "s", "ns", "na", "ss")),
level = 0.5, cex = 1.25,
fill = c(TRUE, FALSE), fill.alpha = 0.05,
xlab = "Student Achievement Test",
ylab = "Peabody Picture Vocabulary Test",
label.pos = c(1, rep(NULL, 5), 1),
xlim = c(-15, 110), ylim = c(40, 110))
# HE Plot for High SES Students:
he1 <- heplot(rohwer.ses1, col=c("red", rep("black",5), "blue"),
hypotheses=list("B=0, High SES" = c("n", "s", "ns", "na", "ss")),
level=0.5, cex=1.25, add=TRUE, error=TRUE,
fill=c(TRUE, FALSE), fill.alpha=0.05,
xlim=c(-15, 110), ylim=c(40,110))
We can also produce an HE plot for the MANCOVA model, which assumes equal slopes:
# Fit model:
rohwer.mod <- lm(cbind(SAT, PPVT, Raven) ~ SES + n + s + ns + na + ss, data=Rohwer)
Anova(rohwer.mod)
##
## Type II MANOVA Tests: Pillai test statistic
## Df test stat approx F num Df den Df Pr(>F)
## SES 1 0.379 12.18 3 60 2.5e-06 ***
## n 1 0.040 0.84 3 60 0.4773
## s 1 0.093 2.04 3 60 0.1173
## ns 1 0.193 4.78 3 60 0.0047 **
## na 1 0.231 6.02 3 60 0.0012 **
## ss 1 0.050 1.05 3 60 0.3770
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
col <- c("red", "black", "gray", "cyan", "magenta", "brown", "darkgreen", "blue")
heplot(rohwer.mod, col=col, xlab="Student Achievement Test",
ylab="Peabody Picture Vocabulary Test", cex.lab=1.25, cex=1.25)
# Add ellipse to test all 5 regressors:
heplot(rohwer.mod, hypotheses=list("Regr" = c("n", "s", "ns", "na", "ss")),
xlab="Student Achievement Test",
ylab="Peabody Picture Vocabulary Test",
cex.lab=1.25, cex=1.25,
col=col, fill=TRUE, fill.alpha=0.1)
We saw when we were working with multiple dependent variables, that it was difficult to visualize more than two at a time or three, if we use an interactive 3D plot. One way that we can circumvent this issu is to utilizae a dimension reduction technique, such as canonical discrimination, to produce a reduced rank display:
library(candisc)
# Using a multivariate regression model, we can produce the canonical discriminant analysis solution:
iris.mod <- lm(cbind(Sepal.Length, Sepal.Width, Petal.Length, Petal.Width) ~ Species, data = iris)
iris.can <- candisc(iris.mod)
# This can be plotted with the generic plot function:
plot(iris.can, col=rep(c("red", "black", "blue"), each=50), pch=rep(1:3, each=50))
# Or as an HE plot:
heplot(iris.can, size = "effect")
Similarly, for the Pottery data:
pottery.mod <- lm(cbind(Al, Fe, Mg, Ca, Na) ~ Site, data=Pottery)
pottery.can <-candisc(pottery.mod)
heplot(pottery.can, var.lwd=3)
Recent advances to this framework have focused upon three areas, visualizing: canonical correlation, robust multivariate models, and influence diagnostics for multivariate models.
Canonical correlationl analysis is a low-rank approximation of multivariate multiple regression, in the same manner than canonican discrimination analysis is a low-rank approximation of a MANOVA. Using the candisc package, we have two approaches to visualizing such an analysis:
library(candisc)
# First, using plot() to show canonical (X, Y) variates as data:
X <- as.matrix(Rohwer[,6:10]) # the PA tests
Y <- as.matrix(Rohwer[,3:5]) # the aptitude/ability variables
(cc <- cancor(X, Y, set.names = c("PA", "Ability")))
##
## Canonical correlation analysis of:
## 5 PA variables: n, s, ns, na, ss
## with 3 Ability variables: SAT, PPVT, Raven
##
## CanR CanRSQ Eigen percent cum scree
## 1 0.6703 0.44934 0.81599 77.30 77.30 ******************************
## 2 0.3837 0.14719 0.17260 16.35 93.65 ******
## 3 0.2506 0.06282 0.06704 6.35 100.00 **
##
## Test of H0: The canonical correlations in the
## current row and all that follow are zero
##
## CanR WilksL F df1 df2 p.value
## 1 0.670 0.440 3.90 15 169 0.0000
## 2 0.384 0.799 1.84 8 124 0.0761
## 3 0.251 0.937 1.41 3 63 0.2488
# Equivalently:
# (cc <- cancor(cbind(SAT, PPVT, Raven) ~ n + s + ns + na + ss, data = Rohwer, set.names=c("PA", "Ability")))
# First canonical dimension (with annotation):
plot(cc, smooth = TRUE, id.n = 3, ellipse.args = list(fill = TRUE), col.smooth = "blue", lwd = 3, cex.lab = 1.4, id.cex = 1.25, pch = 20, cex = 1.5)
text(-2,1.75, "1st Canonical dimension:\n CanR=0.67 (77.3%)", pos = 4, cex = 1.4)
# Second Canonical dimension (with annotation):
plot(cc, which = 2, smooth = TRUE, id.n = 3, ellipse.args = list(fill = TRUE), col.smooth = "blue", lwd = 3, cex.lab = 1.4, id.cex = 1.25, pch = 20, cex = 1.5)
text(-2.9,2.2, "2nd Canonical dimension:\n CanR=0.38 (16.3%)", pos = 4, cex = 1.4)
# Second, using heplot() to show (X, Y) relations as HE plots for Y in canonical space:
heplot(cc, scale = 1.4, var.cex = 1.5, var.lwd = 3, prefix="Y canonical dimension", cex.lab = 1.25, lwd = 2)
A second extension that has been recently advanced is the development of functions that apply robust methods for the fully general multivariate linear model. The heplots package now provides a function, robmlm() to conduct robust MLMs.
As an example, we return to the Pottery dataset:
# Multivariate Model:
pottery.mod <- lm(cbind(Al,Fe,Mg,Ca,Na)~Site, data=Pottery)
# Non-robust ANOVA:
Anova(pottery.mod)
##
## Type II MANOVA Tests: Pillai test statistic
## Df test stat approx F num Df den Df Pr(>F)
## Site 3 1.55 4.3 15 60 2.4e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Robust Multivariate Model:
pottery.rmod <- robmlm(cbind(Al,Fe,Mg,Ca,Na)~Site, data=Pottery)
# Robust ANOVA:
Anova(pottery.rmod)
##
## Type II MANOVA Tests: Pillai test statistic
## Df test stat approx F num Df den Df Pr(>F)
## Site 3 1.98 6.55 15 51 1.7e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
We can visualize how each data point was adjusted using an index plot:
# Basic plot:
plot(pottery.rmod$weights, type = "h", col = "gray", ylab = "Observation Weight", cex.lab = 1.5)
# End points (coloured by site):
points(pottery.rmod$weights, pch = 16, col = Pottery$Site, cex = 1.5)
# Obtain end point locations to plot site names:
prle <- rle(as.numeric(Pottery$Site))
loc <- c(1, cumsum(prle$lengths)[-4])
text(loc, rep(c(-0.01,0.03), length = 4), levels(Pottery$Site)[prle$values], pos = 4, cex = 1.5)
We can also visualize the difference between the robust and the non-robust solution using HE plots:
heplot(pottery.mod, cex = 1.3, lty = 1, cex.lab = 1.4)
heplot(pottery.rmod, add = TRUE, error.ellipse = TRUE, lwd = c(2,2), lty = c(2,2), term.labels = FALSE, err.label = "", fill = TRUE, fill.alpha = 0.1)
legend(15.5, 8.5, c("Classical", "Robust"), col = "blue", lty = c(1,2), bg = 'gray96', cex = 1.6, lwd = 3)
Our final demonstration pertained to visualizing influence diagnostics for multivariate models. Such measures and plots are common for univariate models, but have been unavailable for MLMs. The mvinfluence package provides both measures of influence and methods for plotting them.
library(mvinfluence)
library(heplots)
Rohwer2 <- subset(Rohwer, subset = group == 2)
rownames(Rohwer2) <- 1:nrow(Rohwer2)
# Obtain regression model:
Rohwer.mod <- lm(cbind(SAT, PPVT, Raven) ~ n+s+ns+na+ss, data=Rohwer2)
# Multivariate influence plot for Cook's D vs. Generalized Hat Values:
influencePlot(Rohwer.mod, id.n=3, type="cookd", cex.lab=1.4, id.cex=1.25)
## H Q CookD L R
## 5 0.5682 0.34388 0.84672 1.3160 0.79641
## 10 0.4516 0.03239 0.06339 0.8235 0.05907
## 14 0.1265 0.29968 0.16427 0.1448 0.34308
## 25 0.1571 0.38198 0.26008 0.1864 0.45319
## 27 0.3673 0.21280 0.33866 0.5804 0.33631
## 29 0.3043 0.22950 0.30260 0.4373 0.32987
# Multivariate Leverage/Residual Plot:
influencePlot(Rohwer.mod, id.n=3, type="stres", cex.lab=1.4, id.cex=1.25)
## H Q CookD L R
## 5 0.5682 0.34388 0.84672 1.3160 0.79641
## 10 0.4516 0.03239 0.06339 0.8235 0.05907
## 14 0.1265 0.29968 0.16427 0.1448 0.34308
## 25 0.1571 0.38198 0.26008 0.1864 0.45319
## 27 0.3673 0.21280 0.33866 0.5804 0.33631
## 29 0.3043 0.22950 0.30260 0.4373 0.32987
# Multivariate Likelihood Ratio Plot (log Leverage by log Residual):
influencePlot(Rohwer.mod, id.n=3, type="LR", cex.lab=1.4, id.cex=1.25)
## H Q CookD L R
## 5 0.5682 0.34388 0.84672 1.3160 0.79641
## 10 0.4516 0.03239 0.06339 0.8235 0.05907
## 14 0.1265 0.29968 0.16427 0.1448 0.34308
## 25 0.1571 0.38198 0.26008 0.1864 0.45319
## 27 0.3673 0.21280 0.33866 0.5804 0.33631
## 29 0.3043 0.22950 0.30260 0.4373 0.32987